Boole 대수
Boole 대수는 다음과 같은 공리를 만족하는 2개의 연산자 (+, *)와 원소들의 집합 B에 대해서 정의된 대수적인 구조다.
Boole 대수의 특징
(1) 폐쇄: 연산자 +와 *에 대해서 닫혀있다.
(2) 단위원: 연산자 +와 *에 대한 단위원은 각각 0와 1이다.
| x+0=0+x=x | x*1=1*x=x |
(3) 교환법칙: 모든 x,y∈B 에 대해서
| x+y=y+x | x*y=y*x |
(4) 분배법칙: 모든 x,y∈B 에 대해서
| x*(y+z)=(x*y) +(x*z) | x+(y*z)=(x+y)*(x+z) |
(5) 보수: 모든 원소 x ∈B 에 대하여 x’ ∈B 원소가 존재하여
| x+x’=1 | x*x’=0 |
(6) x!=y를 만족하는 x,y∈B 인 원소가 적어도 2개 이상 존재.
Boole 대수의 성질
> 쌍대성(duality principle)

연산자와 단위원이 교환되어도 Boole 대수의 공리로 부터 추론되는 모든 대수식은 여전히 성립하는 성질.
OR와 AND 연산자들을 교환해주고 1은 0으로, 0은 1로 교환한다.
> 연산자 우선 순위
1. 괄호 2. NOT 3. AND 4. OR
Boole 함수
상수 0/1의 2진 변수와 논리 연산 기호로 구성된 함수. 주어진 2진 변수의 값에 대하여 0이나 1을 나타낸다.
Boole 함수의 표현
진리표로 나타낼 수 있다 - 한 가지 방법 존재
논리 게이트로 구성된 회로로 변환될 수 있다 - 여러 가지 방법 존재
대수 형태로도 나타낼 수 있다 - 여러 가지 방법 존재

> 예시
F_1 = x + y'z

F_2 = x'y'z + x'yz +xy' = x'z(y'+y) + xy' = x'z + xy'


Boole 함수 - 대수적 조작
다음의 Boole 함수를 최소의 리터럴 수로 간략화한다.
(1) x(x'+y) = xx' + xy = 0 + xy = xy.
(2) x +x'y = (x+x')(x+y) = 1(x+y) = x + y.
(3) (x+y)(x+y') = x + xy + xy' + yy' = x(1+y+y') = x.
(4) xy + x'z + yz = xy + x'z + yz(x+x')
= xy + x'z + xyz + x'yz
= xy(1+z) + x'z(1+y)
= xy + x'z
(5) (x+y)(x'+z)(y+z) = (x+y)(x'+z) : 함수 4의 쌍대성에 의함.
(A + B + C)'= (A+x)' B+C=x 로 놓으면
= A'x' Theorem 5(a)의 정리에 의함.
= A'(B+C)' B+C=x 를 대입
= A'(B'C') Theorem 5(a)의 정리에 의함.
= A'B'C' Theorem 4(b)의 정리에 의함.
=> (A+B+C+D+…+F)' = A'B'C'D'…F'
(ABCD…F)' = A' +B'+ C' + D' + … + F'
Boole 함수 - 함수의 보수 구하기
> 예시 (함수의 보수 구하기)
F_1 = x'yz'+x'y'z
F_1' = (x'yz'+x'y'z)' = (x'yz')'(x'y'z)' = (x+y'+z)(x+y+z')
F_2 = x(y'z'+yz)
F_2' = [x(y'z'+yz)]' = x'+(y'z'+yz)' = x'+(y'z')'(yz)' = x'+(y+z)(y'+z')
> 예시 (쌍대성과 각 리터럴의 보수를 사용하여 함수의 보수 구하기)
F_1 = x'yz' + x'y'z.
F_1 의 쌍대는 (x'+y+z')(x'+y'+z)
각 리터럴을 보수화 : (x+y'+z)(x+y+z')=F_1'
F_2 = x(y'z'+yz).
F_2 의 쌍대는 x+(y'+z')(y+z)이다.
각 리터럴을 보수화 : x'+(y+z)(y'+z')=F_2'
정준 형식 (canonical form
진리표에서 얻을 수 있는 기본적인 표현 형식 ( Mi'=mi )
최소항 m(minterm) : 주어진 변수들이 모두 AND 연산으로 조합된 항
최대항 M(maxterm) : 주어진 변수들이 모두 OR 연산으로 조합된 항

> 예시
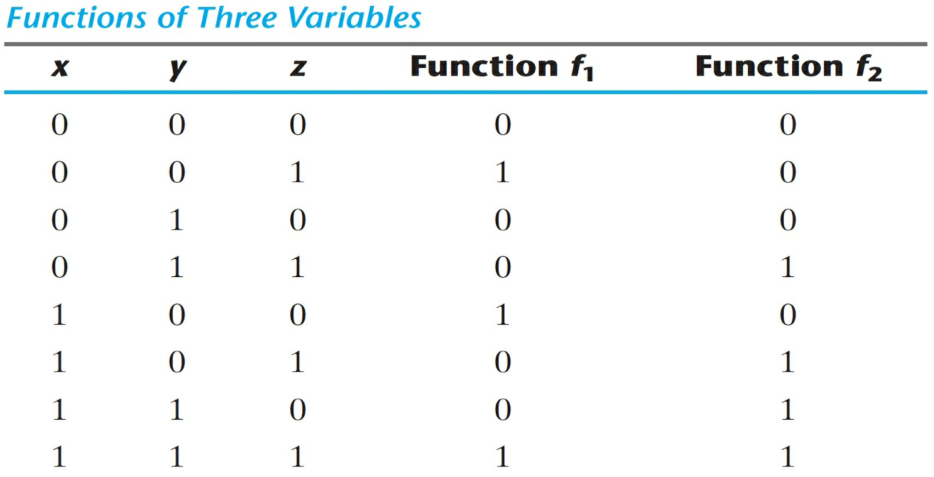
f_1 = x'y'z+xy'z'+xyz = m1+m4+m7
f_2 = x'yz+xy'z+xyz'+xyz = m3+m5+m6+m7
f_1 = (x+y+z)(x+y'+z)(x+y'+z')(x'+y+z')(x'+y'+z) = M0M2M3M5M6
f_2 = (x+y+z)(x+y+z‘)(x+y'+z)(x'+y+z) = M0M1M2M4
정준형식 - 최소항의 합
> 예시 ( Boole 함수 F=A+B'C 를 최소항의 합으로 나타내기 )
A = A(B+B') = AB +AB'
= AB(C+C') + AB'(C+C')
= ABC + ABC' + AB'C +AB'C'
B'C = B'C(A+A') = AB'C + A'B'C
F = A + B'C
= A'B'C + AB'C' + AB'C + ABC' + ABC
= m1 + m4 + m5 + m6 + m7
= ∑(1, 4, 5, 6, 7)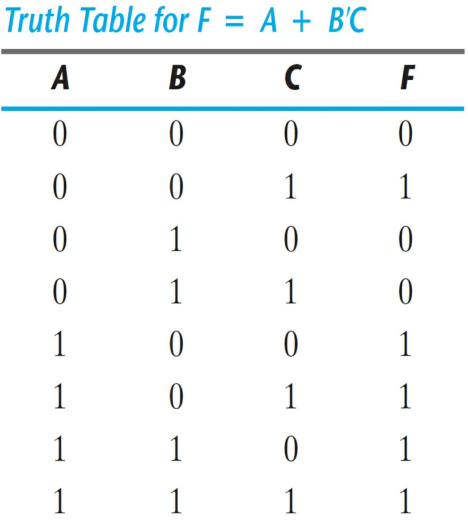
정준형식 - 최소항의 합
> 예시 ( Boole 함수 F = xy + x'z 를 최대항의 곱 형태로 나타내기 )
F = xy + x'z = (xy+x')(xy+z)
= (x+x')(y+x')(x+z)(y+z)
= (x'+y)(x+z)(y+z)
x'+ y= x' + y + zz'= (x'+y+z)(x'+y+z')
x + z= x + z + yy'= (x+y+z)(x+y'+z)
y + z= y + z + xx'= (x+y+z)(x'+y+z)
F = (x+y+z)(x+y'+z)(x'+y+z)(x'+y+z')
= M0M2M4M5
F(x, y, z) = ∏(0, 2, 4, 5)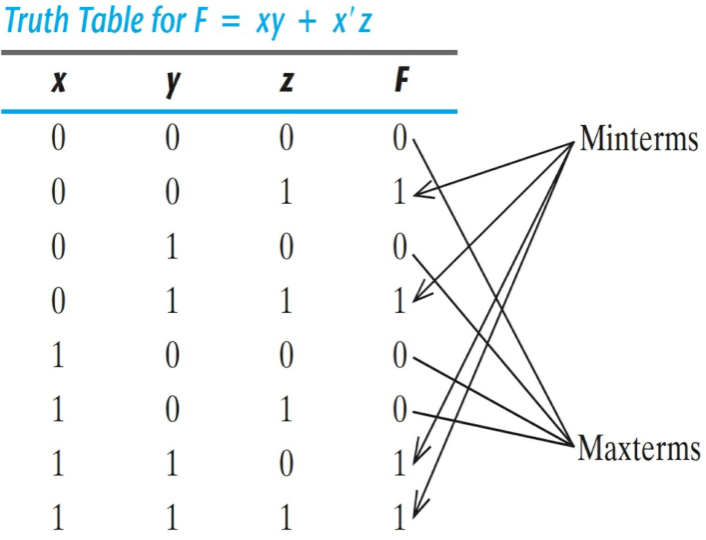
정준형식 사이의 변환
F (A, B, C) = ∑(1, 4, 5, 6, 7)
F'(A, B, C) = ∑(0, 2, 3) = m0 + m2 + m3
F = (m0+m2+m3)' = m0'm2'm3' = M0M2M3 = ∏(0, 2, 3) , mj' = Mj
# 예시
F = xy + x'z
F(x, y, z) = ∑(1, 3, 6, 7)
F(x, y, z) = ∏(0, 2, 4, 5)
표준형식 (standard form)
리터럴의 개수를 최소화시킬 수 없는 정준형식의 단점을 보완한다.

곱의 합 (sum of products) : F1 = y' + x'yz' +xy
합의 곱 (product of sums) : F2 = x(y'+z)(x'+y+z)
> 예시 ( F3 = AB + C(D+E) = AB +CD + CE )

기타 논리 연산들
'전공 수업 CS > Digital Engineering' 카테고리의 다른 글
| [디지털공학] Canonical form 그리고 truth table (0) | 2023.04.05 |
|---|---|
| [디지털공학] 불 함수 관련 용어 정리 (0) | 2023.04.05 |
| [디지털공학] 그레이코드(GRAY CODE) (0) | 2023.03.30 |
| [디지털 공학] 부울식 변환 | 최소항과 최대합 전개 | 일반화 (0) | 2023.03.26 |
| [디지털공학] 부울대수(불대수)란? | Boolean algebra | 쌍대 , 공리, 공준 | 부울 대수의 주요법칙 (0) | 2023.03.26 |
![[디지털공학] 부울 대수와 논리게이트 | Boole 대수](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbEcuwk%2Fbtr6N70tvuc%2FyFhgBKNsAkAzggo8hy6JPk%2Fimg.png)

