이 글은 전공 과목인 디지털 공학을 복습하며 작성한 글이다.
부울함수에 대한 진리표가 주어지면,
표준 논리곱의 합(최소항 전개)과 표준 논리합의 곱(최대항 전개)의 두 가지 함수의 표준 대수식을 얻을 수 있다.
이들을 간략화하여 AND와 OR 게이트로 이루어진 회로를 구성할 수 있게 된다.
부울식 변환
논리설계 문제는 종종 한 문장 혹은 여러 문장을 사용하여 서술되기도 한다.
논리회로 설계의 첫 단계는 이들 문장을 부울식으로 변환하는 것이다.
이렇게 하기 위해서는 각 문장을 구로 나누고 각 구를 부울변수와 연관시켜야 한다.
어떤 한 구가 "참(true)" 혹은 "거짓(false)"의 진리값을 가진다면 이 구는 부울변수로 나타낼 수 있는데,
이와 같은 구는 참 혹은 거짓일 수 있다.
예를 들어보자.
F = 1 if "Mary watches TV" is true; otherwise, F = 0
A = 1 if "it is Monday night" is true; otherwise, A = 0
B = 1 if "she has finished her homework" is true; otherwise, B = 0
A와 B 모두가 "참"일 때 F가 "참"이므로, 이 문장은 다음과 같이 나타낼 수 있다.
F = AB
진리표를 사용하는 조합논리설계
예시를 위해 2진수 N을 가정하도록 하자.
어떤 스위칭회로는 입력이 A, B, C 셋이고, 출력이 하나이다.
A, B, C는 각각 2진수 N의 첫 번째, 두 번째, 세 번째 비트를 나타낸다.
이 회로는 N이 011 이상이면 f =1 이고, 미만이라면 f = 0이다.
이 회로를 대수식으로 표현하기 위해 진리표를 그려보자.
| A B C | f | f' |
| 0 0 0 | 0 | 1 |
| 0 0 1 | 0 | 1 |
| 0 1 0 | 0 | 1 |
| 0 1 1 | 1 | 0 |
| 1 0 0 | 1 | 0 |
| 1 0 1 | 1 | 0 |
| 1 1 0 | 1 | 0 |
| 1 1 1 | 1 | 0 |
이제 이 진리표를 보고 f = 1 인 경우에, A,B,C의 진리값 조합으로 진리표에서 f의 대수식을 구해보자.
A가 0의 값을 가지고, B와 C가 1의 값을 가질때 f = 1이다. 따라서 이는 다음과 같이 표현된다.
A'BC
이와 같이 1이 되는 모든 항을 구해서 OR 연산을 취하도록 하겠다.
(OR 연산을 취하는 이유는 1이 되는 항들 여러개가 있을 때, 단 하나의 항만 1이 되어도 그 값은 1이 나오기 때문)
f = A'BC + AB'C' + AB'C + ABC' + ABC
위 식은 A, B, C의 입력이 011, 100, 101, 110, 111 값들 중 어느 하나일 때 1이 된다.
다른 입력 조합일 때는 식의 5개항 모두가 0이 되기 때문에, f는 0의 값을 가지게 된다.
이제 위 식을 간략화 해보자. 지금까지 배운 부울 대수 정리와 간략화 식을 적용하면 다음과 같이 바뀐다.
f = A + BC
함수를 1에 대하여 구하는 것이 아닌 0에 대하여 구할 수도 있다.
A + B + C 항은 A, B, C 모두가 0인 경우에만 0이 된다.
이런 식으로 0이 되는 항들을 보아 AND하면 다음과 같은 식이 만들어진다.
f = (A + B + C)(A + B + C')(A + B' + C)
이제 위 식도 간략화 하도록 하자.
f = A + BC
최소항과 최대항의 전개
최소항(miniterm)
f = A'BC + AB'C' + AB'C + ABC' + ABC
위 항에서 각 항을 최소항(minterm)이라고 한다.
일반적으로 n개의 변수의 최소항은 각 변수가 그대로 혹은 보수 형태로 단 한 번씩만 나타나는 n개 문자의 곱이다.
최소항은 때때로 간단한 형태로 나타낼 수 있는데, A'B'C'는 m0, A'B'C는 m1으로 나타내는 경우 등이 있다.
일반적으로 진리표의 i번째 행에 해당되는 최소항을 mi라고 한다.
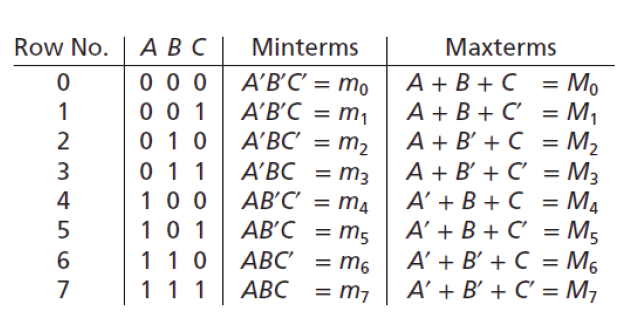
위 사진에서는 최대항(Maxterms)에 대해서도 나와있다.
f = A'BC + AB'C' + AB'C + ABC' + ABC
위의 식처럼 함수 f가 최소항의 합으로 나타낼 수 있을 때,
최소항 전개(minterm expansion) 혹은 표준 논리곱의 합(standard sum of products)으로 되었다고 한다.
진리표의 i번째 행에서 f = 1이면, mi = 1은 입력변수가 진리표의 i번째 행일 때이므로, mi는 최소항 전개에 나타나야 합니다.
f에 있는 최소항은 진리표에서 f가 1인 것과 일대일 대응을 하므로, 함수 f의 최소항 전개는 유일하다.
최소항 전개(혹은 표준 논리곱의 합)와 SOP(곱의 합)에 대한 차이점은 다음과 같다.
SOP(sum-of-products, 곱의합)은 어떠한 식에 존재하는 모든 곱들이 단일 변수들의 곱으로 이루어져 있을 때, 이 식을 곱의합 형식이라고 한다. 중요한 점은 각 항은 존재하는 모든 변수가 사용될 필요 없이, 단지 단일 변수들의 곱으로만 이루어져 있으면 된다.
그에 비해 최소항 전개(minterm expansion) 혹은 표준 논리곱의 합은 n개의 변수가 존재할 때, 식을 이루는 각 항들은 n개의 변수가 모두 단 한 번씩(보수 형태도 가능)나타나는 n개 문자로 이루어진, 즉 최소항들의 합으로 이루어진 식을 최소항 전개되었다고 한다.
f = A'BC + AB'C' + AB'C + ABC' + ABC
위 식을 기호 m을 사용하여 나타내면 다음과 같다.
f(A, B, C) = m_3 + m_4 + m_5 + m_6 + m_7
이 식은 십진수를 나열하는 형식으로 더욱 간단하게 아래와 같이 표현할 수 있습니다.
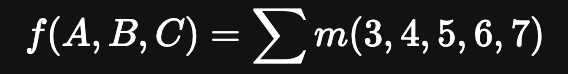
최대항
다음 식을 보도록 하자.
f = (A + B + C)(A + B + C')(A + B' + C)
위 식의 각 항 각각을 최대항(maxterm)이라고 한다.
일반적으로 n개의 변수의 최대항은 각 변수가 그대로 혹은 보수 형태로 한 번씩만 나타나는 n개 문자의 합이다.
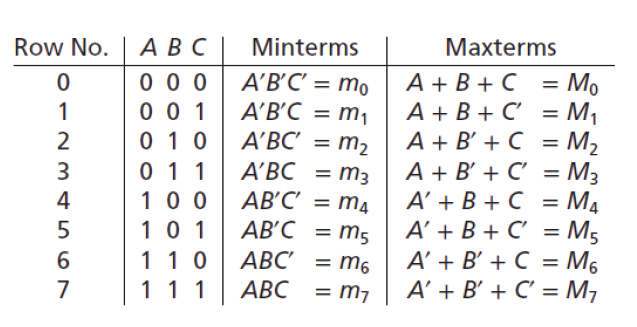
최대항은 보통 기호 M을 사용하여 간단하게 나타낸다.
최소항과 마찬가지로 진리표의 i번째 행에 해당하는 최대항이 Mi이다.
각 최대항은 대응하는 최소항의 보수와 같다. 즉 다음이 성립한다.
M_i = m_i'
함수 f를 아래 식처럼 최대항의 곱으로 나타낼 때 이것을 최대항 전개(maxterm expansion)
혹은 표준 논리합의 곱(standard product of sum)이라 한다.
f = (A + B + C)(A + B + C')(A + B' + C)
위 식을 기호 M을 사용하여 간략화하면 다음과 같다.
f(A,B,C) = M_0M_1M_2
이를 더욱 간단하게 아래와 같이 표현할 수 있다.
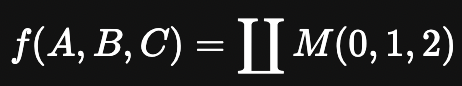
보수
f의 최소항 혹은 최대항 전개가 주어지면 f의 보수에 대한 최소항 혹은 최대항 전개는 쉽게 얻을 수 있다.
f'에 대한 최소항 전개는 f에 빠진 최소항들을 포함하면 된다.
예를 들어

가 주어졌을 때, f'에 대한 최소항 전개는 다음과 같다.
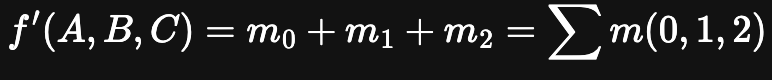
또한 최소항의 보수는 최대항이므로
함수 f에 대한 최대항 전개(maxterm expansion)를 보수화 하면,
함수 f'에 대한 최소항 전개(minterm expansion)을 얻어낼 수 있다.
최소항의 전개를 구하는 방법
최소항 전개를 얻기 위해서는 우선 논리곱의 합(sum of product)으로 식을 작성한 후,
각 항에서 빠진 변수를 X + X' = 1 정리를 사용하여 추가하는 것이다.
또한 f의 최대항을 구하는 방법은 f의 최소항에 해당하지 않는 십진 정수를 열거하여 구할 수 있다.
예를 들어 최소항에 m0, m1, m2, m3 이 사용되었다면, 최대항에는 M4, M5, ...가 사용되는 형식이다.
이 방법 말고도 최대항 전개를 구하는 방법은 다음과 같다.
논리합의 곱(products of sum)을 얻도록 f를 인수분해하고, XX'=0을 적용하여 각 합 항에서 빠진 변수를 추가하여 최대항들을 얻도록 다시 인수분해하는 것이다.
(a + c) -> (a+ bb' + c) -> (a + b + c)(a + b' + c)의 형식이다.
최소항과 최대항 전개의 일반화
아래 표는 세 변수의 일반 함수에 대한 질리표를 보여준다.
각 ai는 0 혹은 1의 값을 갖는 상수이다.
| A B C | F |
| 0 0 0 | a0 |
| 0 0 1 | a1 |
| 0 1 0 | a2 |
| 0 1 1 | a3 |
| 1 0 0 | a4 |
| 1 0 1 | a5 |
| 1 1 0 | a6 |
| 1 1 1 | a7 |
위 표로부터 다음과 같이 세 변수의 일반 함수에 대하여 최소항 전개를 할 수 있다.

ai = 1이면 최소항 mi는 전개에 포함되고, ai = 0이면 mi는 포함되지 않는다.
최대항 전개는 다음과 같다.
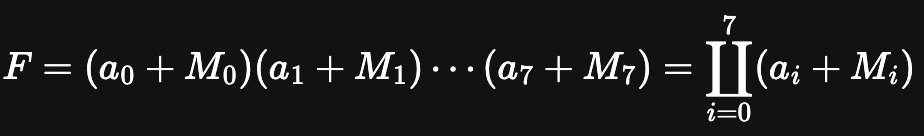
ai = 1 이면 ai + Mi = 1이므로 Mi는 전개에서 빠지지만, ai = 0이면 Mi는 들어간다.
또한 보수에 대해서는 다음과 같다.
보수에 대한 최소항 전개
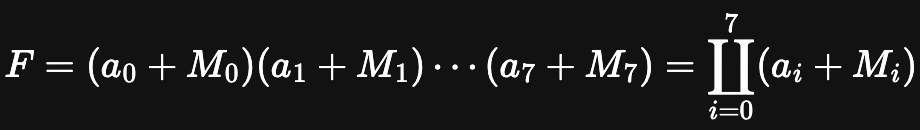

변수의 개수가 n개인 상황으로 일반화하면 다음과 같다.
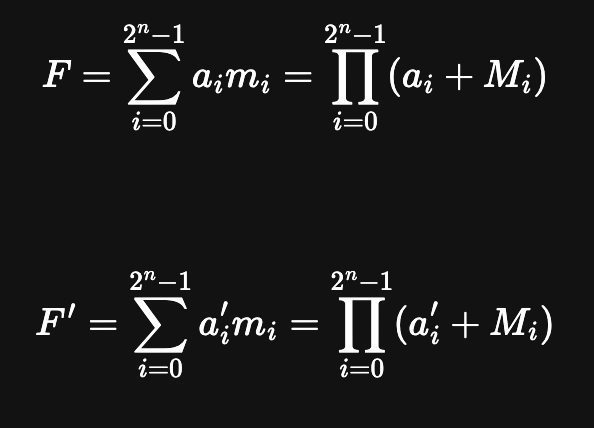
'전공 수업 CS > Digital Engineering' 카테고리의 다른 글
| [디지털공학] 부울 대수와 논리게이트 | Boole 대수 (0) | 2023.03.30 |
|---|---|
| [디지털공학] 그레이코드(GRAY CODE) (0) | 2023.03.30 |
| [디지털공학] 부울대수(불대수)란? | Boolean algebra | 쌍대 , 공리, 공준 | 부울 대수의 주요법칙 (0) | 2023.03.26 |
| [디지털 공학] BCD 코드 | Gray 코드 | 아스키코드 | 여러가지 바이너리 코드 (0) | 2023.03.26 |
| [디지털 공학] 2진수의 부호표기법 | signed number vs unsigned number | 덧셈 보충 (0) | 2023.03.26 |
![[디지털 공학] 부울식 변환 | 최소항과 최대합 전개 | 일반화](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fbb6gtd%2Fbtr5TnB9cjN%2FinWSDYGHQHEU1ck5vWCBv1%2Fimg.png)