이 글은 전공 과목인 디지털 공학 수업을 복습하며 작성하는 글이다.
부울대수 (Boolean Algebra)
대수학 (Algebra)이란 일련의 공리들을 만족하는 수학적 구조들의 일반적인 성질을 연구하는 수학의 한 분야이다.
그 중, 부울대수 (Boolean Algebra)는 참(True), 거짓(False)라는 논리로만 이루어진 대수학이라 할 수 있다.
다들 이미 알다시피 컴퓨터는 0,1 이라는 두개의 숫자만으로 모든 것을 표현한다. True, False라는 논리를 0과 1이라는 두 숫자로 나타낼 수 있기 때문에 부울대수가 컴퓨팅의 기반이 되는 것이다.
논리연산자 - NOT, AND, OR
부울대수를 연산하는 연산자에는 3가지 - NOT, AND, OR - 가 있다. 하나 하나 살펴보도록 하자.
NOT(논리부정)
영어 not의 뜻을 생각하면 연산자 NOT을 쉽게 이해할 수 있다. 알다시피 영어에서 not은 ~가 아니다의 뜻을 가진다.
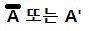
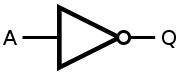
(*게이트란 부울대수 연산을 시각적으로 보기 쉽게 만든 것이다. ex. 변수 A를 게이트에 넣으면 결과값 Q가 나온다.)
A를 NOT 게이트에 넣었을 때 나오는 결과값 Q는 A'가 될 것이다.
AND(논리곱)
영어 and는 그리고 라는 뜻이다. 그러므로 A AND B는 A 그리고 B라는 뜻이 될 것이다. 만약 A AND B의 결과가 True가 되려면 A, B 둘다 True가 되야 할 것이다. 둘 중 하나라도 False라면 True라는 결과가 나올 수 없을 것이다.
| INPUT | OUTPUT | |
| A | B | Q |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
게이트로는 아래와 같이 표현된다.

OR(논리합)
영어 or의 뜻은 또는 이다. 그러므로 A OR B는 A 또는 B라는 뜻이 될 것이다. 만약 A OR B의 결과가 True가 되려면 A, B 둘 중 하나만 True가 되어도 True가 될 것이다.
| INPUT | OUTPUT | |
| A | B | Q |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
게이트로는 아래와 같이 표현된다.

부울대수의 주요 법칙
1. 기본 공리
A⋅A=A, A+A=A, A⋅0=0, A+0=A, A⋅1=A, A+1=1
2. 부정법칙
A⋅A'=0, A+A'=1, A''=A
3. 교환법칙
A⋅B=B⋅A, A+B=B+A
4. 결합법칙
A⋅(B⋅C)=(A⋅B)⋅C, A+(B+C)=(A+B)+C
5. 분배법칙
A⋅(B+C)=A⋅B+A⋅C, A+(B⋅C)=A+B⋅A+C
6. 흡수법칙
A⋅(A+B)=A, A+(A⋅B)=A
- 게이트를 이용하여 직접 계산해보면 왜 이러한 법칙이 성립하는지 이해할 수 있게 된다.
예를 하나 들어보겠다.
A+A'=1
#case1

#case2

다른 법칙도 이런 식으로 직접 연산해보면 왜 그러한 법칙이 성립되는지 이해할 수 있을 것이다.
부울 대수의 공리
공리는 증명을 필요로 하지 않는 전제같은 것이다. 그냥 외우면 된다.
<부울 대수의 공리>
0+0=0 , 0+1=1+0=1 , 1+1=1
0·0=0 , 0·1=1·0=0 , 1·1=1
A=0 이면 A'=1 이고 A=1 이면 A'=0 이다.
부울 대수의 공준과 정리
밑의 표에서 x,y,z등의 문자는 대수적인 변수가 아닌 논리 변수이다. 0과 1이 들어간다.
이 표 역시 외워야한다.

postulate가 공준이고 그 밑으로 6가지 정리가 있다. 빨간 네모안의 내용들 중 드모르간 법칙은 너무 중요하고 나머지 것들은 생소해서 잘 봐두어야하한다. 물론 다 외워야한다.
집합에서 x,y,z,를 주머니라고하고 +를 합집합, ·를 교집합, '를 여집합으로 생각하면 받아들이기 쉬울 것이다.
위의 표에서 (a)와 (b)는 쌍대의 관계를 가지는데 쌍대는 다음과같다.
쌍대
쌍대원리(duality principle ) : 2진 연산자와 단위원이 상호 교환되면 한쪽 부분을 다른 쪽 부분으로부터 얻을 수 있다.
쉽게 말해서 OR연산자(+)와 AND(·)연산자를 서로 바꾸어주고 0을 1로, 1을 0으로 바꾸어주면 된다.
식을 전개할 때나 증명등에 필요하다.
연산자 우선순위
연산자 우선순위가 있다. 불 연산은 다음과 같은 순서로 이뤄진다.
1. 괄호(())
2. NOT(')
3. AND(·)
4. OR(+)
Boolean Function
1. 불 함수(Boolean Function)란?
불 대수는 2진 변수와 논리 연산을 다루는 대수이다. 이런 대수식으로 표현되는 것이 불 함수이다.
내가 배운 것을 토대로 보충하자면 함수가 어떤 변수들의 연산으로 원하는 결과를 이끌어 내듯 불 함수도 0과 1이란 input에서 원하는 결과를 이끌어 내는 논리 변수와 논리 연산의 조합이다.
예시를 들어보겠다.
F1= x+y'z
위의 식이 불 함수이다. 논리 연산인 AND(·)와 OR(+), NOT('), 논리 변수인 x,y,z로 이루어져있다.

Truth Table(진리표)란 각 변수와 함수의 결과를 표로 정리해놓은 것을 말한다.


다른 논리연산이다. 빨간 네모박스에 있는 것은 알아두는 것이 좋다.
Digital design과목의 목표는 말그대로 논리회로를 설계하는 것이다. input에서 원하는 output을 출력해주는 회로를 설계하는 것이 목표이다. 그런 의미에서 불 함수는 매우 중요하다.
'전공 수업 CS > Digital Engineering' 카테고리의 다른 글
| [디지털공학] 그레이코드(GRAY CODE) (0) | 2023.03.30 |
|---|---|
| [디지털 공학] 부울식 변환 | 최소항과 최대합 전개 | 일반화 (0) | 2023.03.26 |
| [디지털 공학] BCD 코드 | Gray 코드 | 아스키코드 | 여러가지 바이너리 코드 (0) | 2023.03.26 |
| [디지털 공학] 2진수의 부호표기법 | signed number vs unsigned number | 덧셈 보충 (0) | 2023.03.26 |
| [디지털 공학] 보수 | 2진수의 산술 연산 | 2진수의 덧셈과 뺄셈 방법 (0) | 2023.03.26 |
![[디지털공학] 부울대수(불대수)란? | Boolean algebra | 쌍대 , 공리, 공준 | 부울 대수의 주요법칙](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FcpnsXO%2Fbtr53DqR8uO%2FqRqKV9cWP8oeqs6Fboyvd1%2Fimg.png)