이 글은 전공과목 디지털 공학을 복습하며 작성한 글이다.

이렇게 게이트 레벨을 최소화 하는 것이 핵심이다. 최소화가 필요한 이유는 이 글 마지막에 간단히 설명할 것이다.
게이트 레벨을 최소화 하기위한 방법은 2가지가 있다.
1. 대수적인 방법
2, K-map(카르노 맵)
대수적인 방법
이 방법은 논리변수가 많지 않을 때 사용하는 방법이다. 앞에서 배운 공준, 기본정리, 연산방법을 이용해 최대한 함수를 간략하게 만들어야한다. 예를 들어보자
F= x'y'z + x'yz+ x'y (a)
위의 식을 간단하게 해보자
앞에서 배웠던 분배법칙[xy+xz=x(y+z)]과 공준[x+x'=1]를 사용해 식을 간략하게 만들 수 있다. 대부분 이 두가지를 사용하여 식을 간단하게 만든다.
F=x'z(y+y')+xy'=x'z+xy' (b)
항의 개수가 줄어든 것을 볼 수 있다.
이것을 논리게이트를 사용해 구현하면
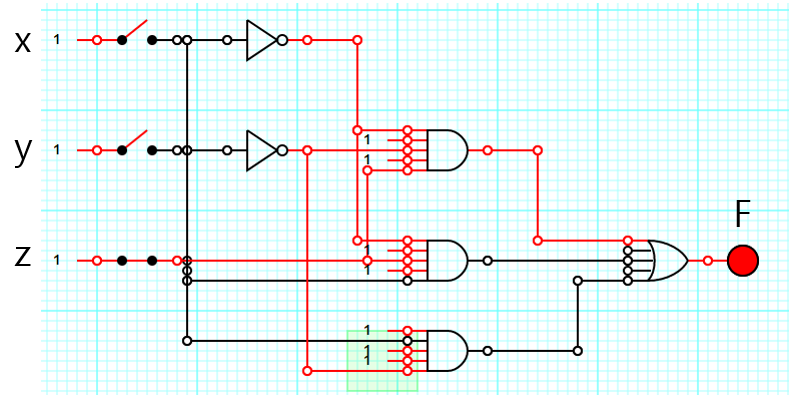
간소화 하면
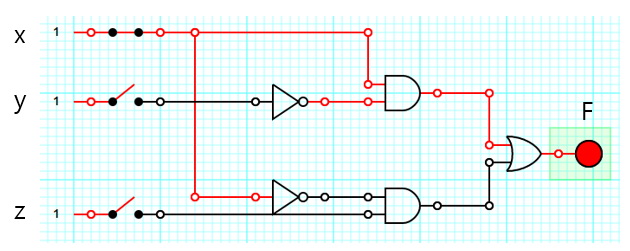
확연히 간단해 진 것을 볼 수 있다. 같은 기능을 수행하는 회로를 더 적은 게이트 수로 만들 수 있다는 것을 알 수 있다.
기본 공식들을 외워놓고 다양한 문제를 풀어보는 것이 이 방법의 핵심이다.
위의 게이트는 https://sciencedemos.org.uk/logic_gates.php에서 그릴 수 있다.
K-map ( 카르노 맵 or 카노 맵 )
우리는 진리표를 보고 canonical form의 불 함수를 조작하여 가장 경제적인 회로를 설계하는 것이 목표이다. 이러한 관점에서 본다면 불 대수를 조작하는 방법은 몇 가지 단점을 가지고 있다.
1. 논리변수가 많아지면 불 대수의 조작이 쉽지않다.
2. 특정한 규칙이 없다.
3. 한개의 식을 간소화 했을 때 어떤 여러가지 식이 나오는 지 모른다.
우리가 회로를 설계할 때 진리표는 무조건 1개지만 그 역할을 수행할 수 있는 함수는 여러개가 나온다. 불 대수 조작할 때 전개 과정에 나오는 식들만 해도 모두 같은 역할을 수행하는 것이다. 불 대수 조작을 하면 한개의 불 함수에서 최적화된 하나의 식밖에 못얻지만 k-map은 여러가지 간소화된 식을 알 수 있다.
1. K-map의 원리
K-map은 불 대수의 조작을 그림으로 표현하므로써 더욱 가시적으로 최소화를 할 수 있도록 하는 일종의 도구이다.
카르노 맵의 구조
2변수 카르노 맵과 4변수 카르노 맵을 예로들어 설명하겠다.

위의 그림이 카르노 맵의 구조이다. 2변수 카르노 맵은 매우 간단하다.
카르노 맵을 그릴 때 규칙이 있다.
인접한 열에서 다음 열로 바뀔 때에는 한 비트만이 바뀐다.
이 규칙의 이유는 이글을 읽다보면 이해가 될 것이다.
이 규칙을 따라 4변수 카르노 맵을 그려본다면

다음과 같은 구조를 순서를 헷갈리지 않게 조심하도록하자.
Truth table과 카르노 맵의 관계
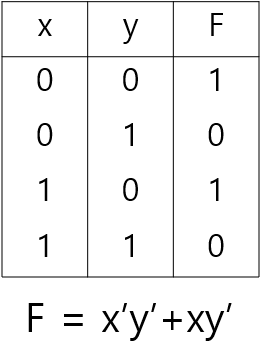
다음 식을 카르노 맵으로 나타내면
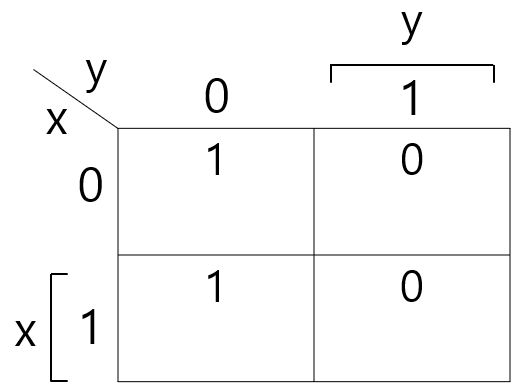
이렇게 된다. Truth table을 보고 해당하는 자리에 0과 1을 넣은 것 뿐이다.
불 대수 조작과 비교하기

그림을 보면 충분히 이해가 될 것 같다. 1을 묶어주는 행위는 불 연산에서 분배법칙을 시행한 것이다. 이 그림을 이해했다면 1비트만 차이나게 그리는 이유를 알 수 있다. 그 이유는 분배법칙을 시행하기 위함이다.
묶인 것을 모두 포함하는 불 변수로 불 함수가 최적화 되는 것을 알 수 있다. 불 연산과 꼭 비교해 보길 바란다. 이해하는데 큰 도움이 될 것이다.
1. K-map의 사용
유의할 점
1. 인접한 열에서 다음 열로 바뀔 때에는 한 비트만이 바뀐다.
2. 1을 묶을 때 2의n개의 수 만큼만 묶을 수 있다.(2,4,8...)
3. 1을 묶을 때 겹치는 것을 신경쓰지 않고 최대한 크게 묶어야한다. 또한 한개의 묶음 안에 다른 묶음이 포함되면 안된다.
4. 양끝, 꼭짓점을 묶을 수 있다는 것을 잊지마라.
1번의 보충설명은 위에 있으므로 넘어간다.
2번 보충설명
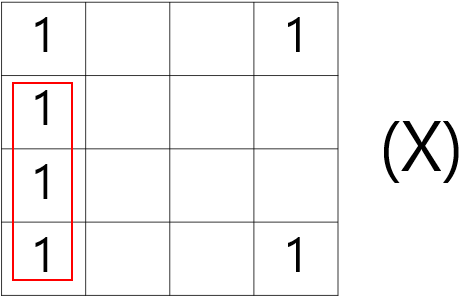
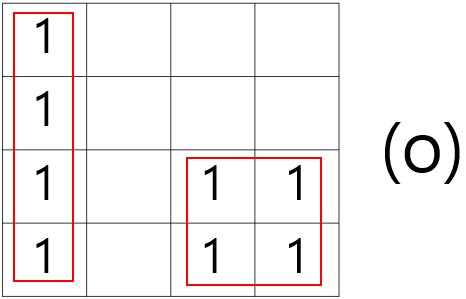
3번 보충설명



4번 보충설명


이렇게 묶을 수 있는 이유는 분배법칙을 위해 1비트만 차이나면 묶을 수 있기 때문이다. 궁금하면 불 연산을 해보길 바란다.
순서
1) Truth table을 보고 1과 0을 카르노맵에 해당하는 자리에 채운다.
2) 모든 1이 묶일 때 까지 최대한 크게 묶는다.
3) 최적화 된 불 함수를 찾는다.
가장 간략화된 수식은 항의 개수가 최소이고 각각의 항이 최소의 리터럴 수를 갖는 식을 의미한다.
카르노 맵을 사용하여 최적화 하는 것은 다음 포스팅에서 예시를 들어 보이겠다.
최소화가 필요한 이유
불 함수가 진리표로 표현될 때는 단 1개의 진리표만 나오지만 진리표를 불 함수로 나타냈을 때 매우 여러가지 불 함수가 나온다. 불 함수는 바로 게이트들의 연결로 반영된다. 설계자들은 회로를 간단하게 설계함으로써 비용을 줄여야하기때문에 회로의 복잡도와 사용되는 게이트를 줄여야한다. 따라서 불 함수를 간략화 하는 것은 경제적으로 매우 중요하다.
다음 포스팅에서는 K-map의 예시를 보여주고 K-map의 나머지 내용을 포스팅 할 것이다.
'전공 수업 CS > Digital Engineering' 카테고리의 다른 글
| [디지털공학] digital design 1장 정리 (0) | 2023.04.05 |
|---|---|
| [디지털공학] 함수의 보수와 Canonical form 사이의 변환 (0) | 2023.04.05 |
| [디지털공학] Canonical form 그리고 truth table (0) | 2023.04.05 |
| [디지털공학] 불 함수 관련 용어 정리 (0) | 2023.04.05 |
| [디지털공학] 부울 대수와 논리게이트 | Boole 대수 (0) | 2023.03.30 |
![[디지털공학] 게이트 레벨 최소화하기 | 대수적 방법, 카르노맵(k-map)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2Fcq7ZNI%2Fbtr7357WeVo%2FAAAAAAAAAAAAAAAAAAAAAFp8ddwLyZigAE4maFb9eAf-b4v2jLSDQFrGfLo1yhfI%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1751295599%26allow_ip%3D%26allow_referer%3D%26signature%3DPkxx131BGh9B8FYzqcUf4BIT2kI%253D)