문자열을 검색하려면? : 패턴 매칭
문자열을 검색하는 상황은 많은 상황에서 쓰입니다.
포털 사이트 키워드 검색에서도 사용될 수 있고, 웹 페이지에서 ctrl+F 를 눌러서 검색하는 데에도 사용될 수 있습니다.
이렇듯 본문이 되는 String에서 찾고자 하는 특정한 String을 패턴이라고도 하는데, 이 패턴을 찾는 방법을 패턴 매칭이라고 합니다.
달리 말해서 패턴 매칭이지, 그냥 문자열 검색이라고 생각하면 됩니다.
SW Expert Academy를 통해 문자열 검색에도 다양한 알고리즘이 있음을 다시 한번 알게 되었습니다.
특정 문자열에서 어떤 키워드를 검색하려면 어떻게 해야 할까요?
1. 고지식한 알고리즘(Brute Force)
말 그대로 고지식하게, 본문이 되는 문자열의 맨 앞에서부터 끝까지, 찾고자 하는 문자열과 하나 하나 비교하는 것입니다.
예를 들어, HELLOMYHEAD 이라는 문자열에서 HEAD 를 찾기로 해 봅시다.

하지만 최악의 경우, 본문이 되는 문자열의 모든 위치에서 찾고자 하는 문자열(패턴)과 비교해야 합니다.
따라서 본문 문자열의 길이를 M, 패턴의 길이를 N이라 한다면 시간복잡도는 O(MN)이 됩니다.
만약 길이가 10000인 문자열에서 길이 80의 패턴을 찾는다고 한다면,
최악의 경우 대략 10000 * 80 = 80만번의 비교를 해야 한다는 말이 됩니다.
그림에서 볼 수 있듯, 초반에 HE 까지는 같았는데 이러한 점을 이용해 비교 횟수를 줄일 수 없을까? 하는 생각을 할 수 있게 됩니다.
● 2. KMP 알고리즘(Knuth Morris Partt Algorithm)
문자 검색 알고리즘으로 많이 등장하는 것이 KMP 알고리즘입니다. (KMP는 만든 사람 이름을 딴 것)
KMP 알고리즘을 한 문장으로 말하자면,
불일치가 발생하기 직전까지 같았던 부분은 다시 비교하지 않고 패턴 매칭(검색)을 진행하자! 는 것입니다.
이렇게 비교 횟수를 줄이고, 검색 알고리즘의 효율성을 높이자는 것이 이 알고리즘의 의도입니다.
KMP 알고리즘을 이해하기 위해 2-1 부터 차례대로 살펴보도록 하겠습니다.
○ 2-1. 접두부, 접미부, 그리고 경계
접두부와 접미부, 경계의 의미를 먼저 알아야, KMP 알고리즘에 대해 이해할 수 있습니다.
(KMP 알고리즘을 설명할 때 접두부, 접미부, 경계 라는 표현을 많이 사용하므로 저도 그렇게 하겠습니다.)
문자열에서 접두부와 접미부는 다음의 경우를 말하며, 접두부와 접미부는 전체 문자열이 될 수는 없습니다.

그리고 경계란 다음과 같이 ‘접두부’와 ‘접미부’ 가 같을 때, 그 접두부 혹은 접미부를 가리킵니다.

이렇게, 주어진 문자에 대한 접두부, 접미부, 경계가 의미하는 바를 알게 되었습니다.
이제 KMP 알고리즘의 순서를 말해 보겠습니다.
○ 2-2. KMP 알고리즘의 순서
- (1) 본문이 되는 문자열(비교할 대상)이 있고, 찾으려는 패턴을 처음에 둡니다.

- (2) 일부가 일치하지 않는다면, 불일치한 부분을 제외한 직전까지 일치하는 패턴에서 최대 길이의 경계를 찾습니다.
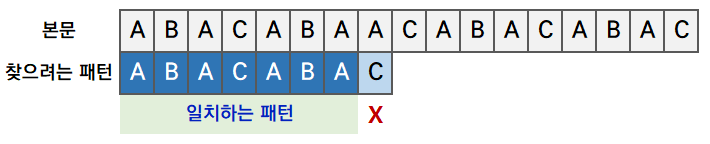
불일치 부분을 제외하고 본문과 일치하는 패턴이 ABACABA 이므로, 이 패턴에서 경계를 찾습니다.
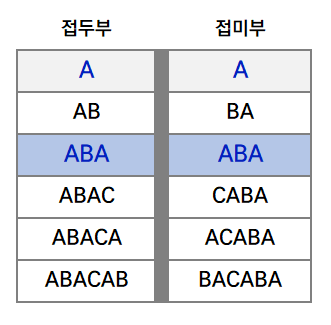
그런데, 경계가 위처럼 두 가지 이상 나올 수도 있는데, 이 때는 경계의 길이가 “최대”가 될 때를 선택합니다!!
- (3) 선택한 경계에서 접두부, 접미부를 파악하고 찾으려는 패턴을 접미부의 시작 문자열까지 이동시킵니다.

그리고 1번부터 다시 과정을 반복합니다.
- ※ 2 에서 경계를 찾지 못하거나, 모두 불일치할 경우
만약 2번에서 경계를 찾지 못하였다면, 처음으로 불일치했던 부분까지 패턴을 이동시킵니다.
그리고 1번부터 다시 과정을 반복합니다.
이렇듯 최대 경계가 되는 경우를 찾아서 접두부를 접미부까지 이동시키거나, 경계를 찾지 못한다면 불일치한 부분만큼 이동시킬 수 있으므로, 고지식한 알고리즘(Brute Force)보다 훨씬 효율적입니다.
그런데 매번 움직일 때마다 경계를 찾으려면 접두부, 접미부를 반복적으로 분석해야 할 것이며, 이는 KMP 알고리즘의 효율성을 떨어트립니다.
따라서 이동시킬 때 참고할 수 있는 이동 경로 테이블을 만들어야 합니다.
○ 2-3. 이동경로 테이블 만들기
이동 경로 테이블이란, 얼마나 이동시켜야 하는지 알 수 있게 하는 테이블입니다.

각 테이블에 들어갈 항목에 대한 설명입니다.
- 일치하는 패턴의 길이 : 본문과 찾으려는 패턴을 맨 앞에서부터 비교하여 어느 지점에서 불일치가 발생하였다면, 그 직전까지 일치하는 패턴의 길이
- 최대 경계 너비 : 본문과 패턴 간에 일치하는 부분에서 경계를 찾고, 그들 중 최대의 길이값

이동거리는 위와 같이 구합니다.
왜 이런 방식으로 계산하는지는 2-2. KMP 알고리즘의 순서의 그림들을 살펴보면서 대입해 본다면 바로 알 수 있습니다.
이제 위에서 새로 든 예시인 ABACABAAC 를 가지고 테이블을 만들어 보겠습니다.
- 일치하는 패턴의 길이가 0일 때
- 본문과 패턴이 처음부터 다르다면, 패턴은 한 칸만 이동시켜야 하므로, 이동거리 공식에 의해서 최대 경계 너비값을 -1로 설정합니다.
- 일치하는 패턴의 길이가 1일 때
- A 에서 경계를 찾을 수 없으므로 최대 경계 너비값은 0
- 일치하는 패턴의 길이가 2일 때
- AB 에서 경계를 찾을 수 없으므로 최대 경계 너비값은 0
- 일치하는 패턴의 길이가 3일 때
- ABA 에서 경계는 A 하나만 나오고 이 때의 접두부(접미부) 길이 = 최대 경계 너비값 = 1
- 일치하는 패턴의 길이가 4일 때
- ABAC에서 경계를 찾을 수 없으므로 최대 경계 너비값은 0
- 일치하는 패턴의 길이가 5일 때
- ABACA에서 경계는 A 하나만 나오고 이 때 최대 경계 너비값 = 1
- 일치하는 패턴의 길이가 6일 때
- ABACAB에서 경계는 AB 하나만 나오고 이 때 최대 경계 너비값 = 2
- 일치하는 패턴의 길이가 7일 때
- ABACABA에서 경계를 찾으면
- 접두부, 접미부가 A 일 때
- 접두부, 접미부가 ABA 일 때
- 이 둘 중에서 최대 길이의 경계는 ABA 일 때이며, 이 때 최대 경계 너비값은 = 3
- ABACABA에서 경계를 찾으면
- 일치하는 패턴의 길이가 8일 때
- ABACABAA에서 경계를 찾으면 A 하나만 나오고 이 때 최대 경계 너비값 = 1
- 일치하는 패턴의 길이가 9일 때
- 찾으려는 패턴 9글자가 모두 일치하므로 찾기 완료!
- 그러나, 그 뒤에도 찾으려는 패턴과 일치하는 경우가 더 있을 수 있으므로 마찬가지로 최대 경계 너비를 계산하여 채운다.
- ABACABAAC 에서 경계를 찾을 수 없으므로 최대 경계 너비값은 0
- 찾으려는 패턴 9글자가 모두 일치하므로 찾기 완료!
표를 완성하면 다음과 같습니다.

이제 표에 근거하여 패턴 매칭을 진행해 보겠습니다.

- 일치하는 패턴의 길이가 7 이므로, 표에서 최대 경계 너비값을 읽습니다. = 3
- 이동 거리는 일치하는 패턴의 길이 - 최대 경계 너비 이므로 7 - 3 = 4칸을 이동합니다.

- 4칸 이동한 후에는 일치하는 패턴의 길이가 ABACABA 까지 7이므로, 표를 확인한 후 이동거리를 계산하면 7 - 3 = 4칸 이동합니다.

- 4칸 이동한 후 살펴보니 모두 일치하므로 패턴 매칭(검색)을 완료합니다.
- 코딩 시 반복문은 본문의 길이만큼 제한할 것이므로, 본문이 더욱 길다면 패턴 매칭을 계속 진행할 것입니다.
'전공 수업 CS > algorithms' 카테고리의 다른 글
| [알고리즘] 스트링 처리 알고리즘 | 패턴 매칭 알고리즘 (0) | 2022.11.10 |
|---|---|
| [알고리즘] 스트링 처리 알고리즘 | 보이어 무어 알고리즘 (0) | 2022.11.10 |
| [알고리즘] 쉘 정렬 알고리즘 (1) | 2022.10.11 |
| [알고리즘] 삽입 정렬 알고리즘 (1) | 2022.10.11 |
| [알고리즘] 버블정렬 (0) | 2022.10.11 |
![[알고리즘] 스트링 처리 알고리즘 | KMP 알고리즘](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2Fbc1crm%2FbtrQPLr966K%2FAAAAAAAAAAAAAAAAAAAAAJgDjMBFps2xJCYoI5uZnSkf4g8MhURrYo3xUUwtLRXg%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3DPrVkgKK5VwITjpGfdXxTvjOvv3g%253D)