오늘부터 알고리즘을 차근차근 공부할 생각이다.
매주 두 가지 주제의 알고리즘을 정복해나가는 식으로 공부할 예정이다.
10/4 (수요일) ~10/ 10 (화요일) 동안 공부할 알고리즘은 그리디 알고리즘과 스택, 큐 덱(자료구조)를 이용한 알고리즘이다.
오늘은 일단 내 생일 1004이므로 그리디 알고리즘을 간략하게 공부하고 백준 한 문제를 푸는 것으로 마무리 해야겠다.
그리디 알고리즘
그리디 알고리즘은 가장 직관적인 알고리즘 설계 패러다임 중 하나이다. 이는 우리가 원하는 답을 재귀 호출과 똑같이 여러 개의 조각으로 쪼개고, 각 단계마다 답의 한 부분을 만들어 간다는 점에서 완전 탐색이나 동적 계획법 알고리즘과 다를 것이 없다. 그러나 모든 선택지를 고려해 보고 그중 전체 답이 가장 좋은 것을 찾는 두 방법과는 달리, 탐욕법은 각 단계마다 지금 당장 가장 좋은 방법만을 선택한다. 지금의 선택이 앞으로 남은 선택들에 어떤 영향을 끼칠지 고려하지 않는다는 것이다.
- 탐욕법을 사용해도 항상 최적해를 구할 수 있는 문제를 만난 경우, 탐욕법은 동적 계획법보다 수행 시간이 훨씬 빠르기 때문에 유용하다.
- 시간이나 공간적 제약으로 인해 다른 방법으로 최적해를 찾기 너무 어렵다면 최적해 대신 적당히 괜찮은 답(근사해)을 찾는 것으로 타협할 수 있다. 이럴 때 최적은 아니지만 임의의 답보다는 좋은 답을 구하는 용도로 유용하게 쓰인다.

위와 같은 예시에서 우선 A에서 다음 위치로 가는 경우를 찾아야 한다. 그 선택을 할 때는, A, B, C, D의 4개만 보고 선택을 하게 된다.
A - E로 가는 3가지 경로가 있을 때, 가장 먼저 A에서 B/C/D 중 최적 경로는 C로 가는 길이다. 그러나 C-E는 150이 걸리기 때문에 실제로는 A - B - E가 최적 경로가 된다.
최초의 선택에서 최적 선택을 하여 부분 최적해는 구했지만 전체 선택에서는 오히려 최적이 아닌 경로를 선택하여 전체 문제에서의 최적값은 구하지 못하게 된 것이다.
그럼에도 불구하고 그리디 알고리즘은 속도가 매우 빠르기 때문에 자주 사용될 수 있다. 하지만 항상 최적해가 되지 않으므로 특수한 조건이 만족되어야 사용할 수 있다.
아래와 같이 2가지 조건을 만족해야 한다.
1) 탐욕 선택 속성(Greedy Choice Property)
2) 최적 부분 구조(Optimal Substructure)
1)은 이전의 선택이 이후에 영향을 주지 않음을 의미하며, 2)는 부분 문제의 최적결과가 전체에도 그대로 적용될 수 있어야 한다는 것이다.
2)의 조건에서 우리는 Dynamic Programming을 떠올릴 수 있다. 실제로 DP에서도 이와 같은 조건이 필요하기 때문이다. 하지만 DP는 다른 조건이 다르다.(DP관련 포스팅은 여기를 참조)
DP의 경우에는 문제가 Overlapping되기 때문에 다음에 풀 문제가 이전의 작은 문제의 결과에 영향을 받게 된다. 즉, 동일한 형식의 문제가 점점 커질 뿐, 이전의 경우에 영향을 받는다.
하지만 그리디 알고리즘은 이와 달리 영향을 받아서는 안된다. 그래야 다른 경우의 결과에 상관 없이 최적해를 구할 수 있기 때문이다.
그런데 위의 2가지 조건을 완전히 만족하는지, 그래서 해당 문제가 그리디 알고리즘을 사용할 수 있는 경우인지를 증명하는 것은 좀 어렵다.
일반적으로 그리디임을 증명하려면 수학적 증명이 동반되어야 한다. 하지만 이 방식은 좀 어려우므로 우선 테스트 코드를 작성하여 정상 동작하는지를 알아보는 방식으로 시도하는 경우가 많다.
그리디가 아니라고 보는 경우는 반례를 1개만 찾아도 되기 때문에 상대적으로 쉽다.
2) 예시 - Action Selection 문제
그리디 알고리즘의 가장 대표적인 예시인 활동 선택(Action Selection) 문제에 대해서 알아보자.
활동 선택 문제는 N개의 활동이 있고 각 활동에는 시작 시간 및 종료 시간이 있을 때, 한 사람이 최대한 많이 할 수 있는 활동(Activity)의 수를 구하는 문제이다.
즉, 각각의 활동(Activity)에는 시간이 소요되므로 하나를 선택했다면 그 동안 해당 시간에 다른 Activity를 할 수 없다. 이러한 상황일 때 가장 많은 활동에 참여하려면 어떻게 해야 할까?
아래의 그림을 보자.

위에서 각 활동과 그것들의 시작 / 종료 시간이 설정되어 있는 것을 알 수 있다. 이 문제는 최대한 많은 활동을 해야 하므로 언제 시작하든 전체에서 가장 종료 시간이 빠른 것부터 선택해야 한다.
어차피 시작 시간은 종료 시간 이전이므로 고려하지 않는다.
따라서, 종료 시간을 기준으로 정렬한 뒤, 제일 먼저 끝나는 활동을 무조건 선택하고 끝났을 때, 바로 다음에 선택할 수 있는 활동을 찾아 수행하는 방식을 반복하여 해결할 수 있다.
아래의 그림을 통해 해결 방법을 알아보자.
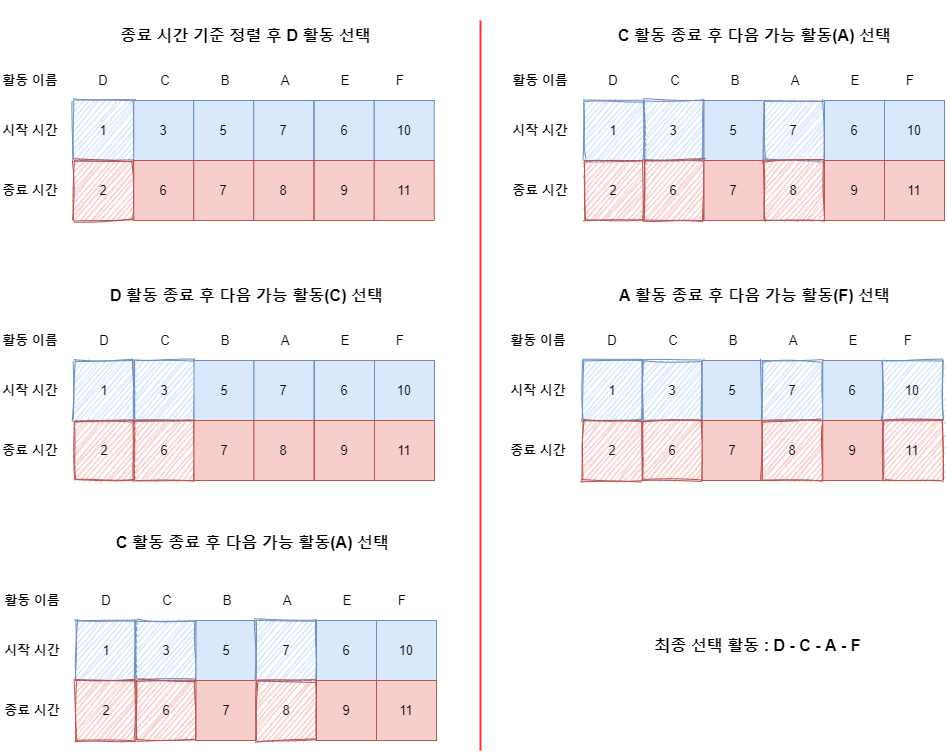
좌측 부터 수행 후 우측 그림과 같이 수행이 완료되어 최종 D - C - A - F 번째 활동을 선택하게 된다.
코드로 풀어보기
import java.util.ArrayList;
import java.util.Collections;
public class Main{
public static void main(String[] args){
// 활동 정보를 List에 저장하고 정렬한다.
ArrayList<Action> list = new ArrayList<>();
list.add(new Action("A", 7, 8));
list.add(new Action("B", 5, 7));
list.add(new Action("C", 3, 6));
list.add(new Action("D", 1, 2));
list.add(new Action("E", 6, 9));
list.add(new Action("F", 10, 11));
Collections.sort(list);
// Greedy 알고리즘 수행 후, 결과 출력
ArrayList<Action> ans = greedy(list);
for(Action act : ans){
System.out.print(act.name + ", ");
}
}
// Greedy 알고리즘을 통해 선택된 활동들을 반환한다.
private static ArrayList<Action> greedy(ArrayList<Action> list){
int time = 0;
ArrayList<Action> ans = new ArrayList<>();
for(Action act : list){
if(time <= act.startTime){
time = act.endTime;
ans.add(act);
}
}
return ans;
}
}
// 활동 정보를 가진 Class로 Comparable을 구현하여 종료 시간 기준 오름차순으로 정렬함.
class Action implements Comparable<Action>{
String name;
int startTime;
int endTime;
public Action(String name, int startTime, int endTime){
this.name = name;
this.startTime = startTime;
this.endTime = endTime;
}
@Override
public int compareTo(Action a) {
return this.endTime - a.endTime;
}
@Override
public String toString() {
return this.name;
}
}
// 결과
// D, C, A, F,
3) 예시 - 거스름돈 문제
이번엔 돈을 낸 뒤, 거스름돈을 최소 개수의 동전 및 지폐의 조합으로 주는 경우, 그 개수를 구하는 문제에 대해서 알아보자.
예를 들어, 누군가 2,730원 어치의 물건을 사고 5,000원을 냈다고 가정하면 거스름돈은 총 2,270원이 될 것이다. 이 때, 지폐와 동전 종류가 아래와 같을 때, 최소의 개수로 거스름돈을 주는 경우는 어떤 경우일까?
지폐 및 동전의 종류 : 1,000원, 500원, 100원, 50원, 10원
정답 : 1,000원 2개 / 100원 2개 / 50원 1개 / 10원 2개로 총 7개
이를 풀어낸 원리는 기본적으로 MSD를 이용한 것이다.(이는 Radix 정렬 관련 포스팅에서 다룬 바 있다. 여기 참조)
MSD는 Most Significant Digit이란 의미로 가장 중요한 단위를 먼저 계산하는 것이다. 위의 경우에서 자신보다 더 큰 지폐 혹은 동전으로 거스름돈을 준다면 나머지는 무조건 더 적은 개수로 반환하는 것이 가능하기 때문에 이를 사용할 수 있다.
따라서, 이전의 선택과 관련 없이 현재 상태에서 최선의 결과를 선택하여 전체에서 최적의 결과를 낼 수 있게 된다.
그런데, 이 문제가 언제나 적용 가능할까? 그렇지 않다.
예를 들어, 거스름돈이 120원을 줘야 하는 상태에서 거스름돈으로 줄 수 있는 동전의 종류가 다음과 같다고 하자.
동전의 종류 : 50원, 40원, 10원
이 때, MSD 방식을 그대로 적용하여 구하면 답은 어떻게 될까?
답 : 50원 2개, 10원 2개로 총 4개
그런데, 실제로 이 문제는 40원 3개를 거슬러 주면 더 적은 개수로 거스름돈을 줄 수 있게 된다.
이전과 다른 점은 무엇일까..? 40원은 자신보다 큰 동전(50원)의 약수가 아니다. 그래서 50원은 40원을 대체해 더 적은 숫자로 반환하는 경우라고 보장할 수 없게 된다.
이와 같이, 그리디 알고리즘으로 해결할 수 있으려면 조건을 충분히 만족하는지를 검증할 수 있어야 한다. 이를 주의하면서 문제를 풀어보자.
